Theorem Proving¶
Equality¶
Idris allows propositional equalities to be declared, allowing theorems about programs to be stated and proved. Equality is built in, but conceptually has the following definition:
data (=) : a -> b -> Type where
Refl : x = x
Equalities can be proposed between any values of any types, but the only way to construct a proof of equality is if values actually are equal. For example:
fiveIsFive : 5 = 5
fiveIsFive = Refl
twoPlusTwo : 2 + 2 = 4
twoPlusTwo = Refl
The Empty Type¶
There is an empty type, 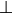 , which has no constructors. It is
therefore impossible to construct an element of the empty type, at least
without using a partially defined or general recursive function (see
Section Totality Checking for more details). We can therefore use the
empty type to prove that something is impossible, for example zero is
never equal to a successor:
, which has no constructors. It is
therefore impossible to construct an element of the empty type, at least
without using a partially defined or general recursive function (see
Section Totality Checking for more details). We can therefore use the
empty type to prove that something is impossible, for example zero is
never equal to a successor:
disjoint : (n : Nat) -> Z = S n -> Void
disjoint n p = replace {P = disjointTy} p ()
where
disjointTy : Nat -> Type
disjointTy Z = ()
disjointTy (S k) = Void
There is no need to worry too much about how this function works —
essentially, it applies the library function replace, which uses an
equality proof to transform a predicate. Here we use it to transform a
value of a type which can exist, the empty tuple, to a value of a type
which can’t, by using a proof of something which can’t exist.
Once we have an element of the empty type, we can prove anything.
void is defined in the library, to assist with proofs by
contradiction.
void : Void -> a
Simple Theorems¶
When type checking dependent types, the type itself gets normalised.
So imagine we want to prove the following theorem about the reduction
behaviour of plus:
plusReduces : (n:Nat) -> plus Z n = n
We’ve written down the statement of the theorem as a type, in just the same way as we would write the type of a program. In fact there is no real distinction between proofs and programs. A proof, as far as we are concerned here, is merely a program with a precise enough type to guarantee a particular property of interest.
We won’t go into details here, but the Curry-Howard correspondence [1]
explains this relationship. The proof itself is trivial, because
plus Z n normalises to n by the definition of plus:
plusReduces n = Refl
It is slightly harder if we try the arguments the other way, because
plus is defined by recursion on its first argument. The proof also works
by recursion on the first argument to plus, namely n.
plusReducesZ : (n:Nat) -> n = plus n Z
plusReducesZ Z = Refl
plusReducesZ (S k) = cong (plusReducesZ k)
cong is a function defined in the library which states that equality
respects function application:
cong : {f : t -> u} -> a = b -> f a = f b
We can do the same for the reduction behaviour of plus on successors:
plusReducesS : (n:Nat) -> (m:Nat) -> S (plus n m) = plus n (S m)
plusReducesS Z m = Refl
plusReducesS (S k) m = cong (plusReducesS k m)
Even for trivial theorems like these, the proofs are a little tricky to construct in one go. When things get even slightly more complicated, it becomes too much to think about to construct proofs in this ‘batch mode’.
Idris provides interactive editing capabilities, which can help with building proofs. For more details on building proofs interactively in an editor, see Theorem Proving.
Theorems in Practice¶
The need to prove theorems can arise naturally in practice. For example,
previously (Views and the “with” rule) we implemented natToBin using a function
parity:
parity : (n:Nat) -> Parity n
However, we didn’t provide a definition for parity. We might expect it
to look something like the following:
parity : (n:Nat) -> Parity n
parity Z = Even {n=Z}
parity (S Z) = Odd {n=Z}
parity (S (S k)) with (parity k)
parity (S (S (j + j))) | Even = Even {n=S j}
parity (S (S (S (j + j)))) | Odd = Odd {n=S j}
Unfortunately, this fails with a type error:
When checking right hand side of with block in views.parity with expected type
Parity (S (S (j + j)))
Type mismatch between
Parity (S j + S j) (Type of Even)
and
Parity (S (S (plus j j))) (Expected type)
The problem is that normalising S j + S j, in the type of Even
doesn’t result in what we need for the type of the right hand side of
Parity. We know that S (S (plus j j)) is going to be equal to
S j + S j, but we need to explain it to Idris with a proof. We can
begin by adding some holes (see Holes) to the definition:
parity : (n:Nat) -> Parity n
parity Z = Even {n=Z}
parity (S Z) = Odd {n=Z}
parity (S (S k)) with (parity k)
parity (S (S (j + j))) | Even = let result = Even {n=S j} in
?helpEven
parity (S (S (S (j + j)))) | Odd = let result = Odd {n=S j} in
?helpOdd
Checking the type of helpEven shows us what we need to prove for the
Even case:
j : Nat
result : Parity (S (plus j (S j)))
--------------------------------------
helpEven : Parity (S (S (plus j j)))
We can therefore write a helper function to rewrite the type to the form we need:
helpEven : (j : Nat) -> Parity (S j + S j) -> Parity (S (S (plus j j)))
helpEven j p = rewrite plusSuccRightSucc j j in p
The rewrite ... in syntax allows you to change the required type of an
expression by rewriting it according to an equality proof. Here, we have
used plusSuccRightSucc, which has the following type:
plusSuccRightSucc : (left : Nat) -> (right : Nat) -> S (left + right) = left + S right
We can see the effect of rewrite by replacing the right hand side of
helpEven with a hole, and working step by step. Beginning with the following:
helpEven : (j : Nat) -> Parity (S j + S j) -> Parity (S (S (plus j j)))
helpEven j p = ?helpEven_rhs
We can look at the type of helpEven_rhs:
j : Nat
p : Parity (S (plus j (S j)))
--------------------------------------
helpEven_rhs : Parity (S (S (plus j j)))
Then we can rewrite by applying plusSuccRightSucc j j, which gives
an equation S (j + j) = j + S j, thus replacing S (j + j) (or,
in this case, S (plus j j) since S (j + j) reduces to that) in the
type with j + S j:
helpEven : (j : Nat) -> Parity (S j + S j) -> Parity (S (S (plus j j)))
helpEven j p = rewrite plusSuccRightSucc j j in ?helpEven_rhs
Checking the type of helpEven_rhs now shows what has happened, including
the type of the equation we just used (as the type of _rewrite_rule):
j : Nat
p : Parity (S (plus j (S j)))
_rewrite_rule : S (plus j j) = plus j (S j)
--------------------------------------
helpEven_rhs : Parity (S (plus j (S j)))
Using rewrite and another helper for the Odd case, we can complete
parity as follows:
helpEven : (j : Nat) -> Parity (S j + S j) -> Parity (S (S (plus j j)))
helpEven j p = rewrite plusSuccRightSucc j j in p
helpOdd : (j : Nat) -> Parity (S (S (j + S j))) -> Parity (S (S (S (j + j))))
helpOdd j p = rewrite plusSuccRightSucc j j in p
parity : (n:Nat) -> Parity n
parity Z = Even {n=Z}
parity (S Z) = Odd {n=Z}
parity (S (S k)) with (parity k)
parity (S (S (j + j))) | Even = helpEven j (Even {n = S j})
parity (S (S (S (j + j)))) | Odd = helpOdd j (Odd {n = S j})
Full details of rewrite are beyond the scope of this introductory tutorial,
but it is covered in the theorem proving tutorial (see Theorem Proving).
Totality Checking¶
If we really want to trust our proofs, it is important that they are defined by total functions — that is, a function which is defined for all possible inputs and is guaranteed to terminate. Otherwise we could construct an element of the empty type, from which we could prove anything:
-- making use of 'hd' being partially defined
empty1 : Void
empty1 = hd [] where
hd : List a -> a
hd (x :: xs) = x
-- not terminating
empty2 : Void
empty2 = empty2
Internally, Idris checks every definition for totality, and we can check at
the prompt with the :total command. We see that neither of the above
definitions is total:
*Theorems> :total empty1
possibly not total due to: empty1#hd
not total as there are missing cases
*Theorems> :total empty2
possibly not total due to recursive path empty2
Note the use of the word “possibly” — a totality check can, of course, never be certain due to the undecidability of the halting problem. The check is, therefore, conservative. It is also possible (and indeed advisable, in the case of proofs) to mark functions as total so that it will be a compile time error for the totality check to fail:
total empty2 : Void
empty2 = empty2
Type checking ./theorems.idr
theorems.idr:25:empty2 is possibly not total due to recursive path empty2
Reassuringly, our proof in Section The Empty Type that the zero and successor constructors are disjoint is total:
*theorems> :total disjoint
Total
The totality check is, necessarily, conservative. To be recorded as
total, a function f must:
- Cover all possible inputs
- Be well-founded — i.e. by the time a sequence of (possibly
mutually) recursive calls reaches
fagain, it must be possible to show that one of its arguments has decreased. - Not use any data types which are not strictly positive
- Not call any non-total functions
Directives and Compiler Flags for Totality¶
By default, Idris allows all well-typed definitions, whether total or not. However, it is desirable for functions to be total as far as possible, as this provides a guarantee that they provide a result for all possible inputs, in finite time. It is possible to make total functions a requirement, either:
- By using the
--totalcompiler flag. - By adding a
%default totaldirective to a source file. All definitions after this will be required to be total, unless explicitly flagged aspartial.
All functions after a %default total declaration are required to
be total. Correspondingly, after a %default partial declaration, the
requirement is relaxed.
Finally, the compiler flag --warnpartial causes to print a warning
for any undeclared partial function.
Totality checking issues¶
Please note that the totality checker is not perfect! Firstly, it is necessarily conservative due to the undecidability of the halting problem, so many programs which are total will not be detected as such. Secondly, the current implementation has had limited effort put into it so far, so there may still be cases where it believes a function is total which is not. Do not rely on it for your proofs yet!
Hints for totality¶
In cases where you believe a program is total, but Idris does not agree, it is
possible to give hints to the checker to give more detail for a termination
argument. The checker works by ensuring that all chains of recursive calls
eventually lead to one of the arguments decreasing towards a base case, but
sometimes this is hard to spot. For example, the following definition cannot be
checked as total because the checker cannot decide that filter (< x) xs
will always be smaller than (x :: xs):
qsort : Ord a => List a -> List a
qsort [] = []
qsort (x :: xs)
= qsort (filter (< x) xs) ++
(x :: qsort (filter (>= x) xs))
The function assert_smaller, defined in the Prelude, is intended to
address this problem:
assert_smaller : a -> a -> a
assert_smaller x y = y
It simply evaluates to its second argument, but also asserts to the
totality checker that y is structurally smaller than x. This can
be used to explain the reasoning for totality if the checker cannot work
it out itself. The above example can now be written as:
total
qsort : Ord a => List a -> List a
qsort [] = []
qsort (x :: xs)
= qsort (assert_smaller (x :: xs) (filter (< x) xs)) ++
(x :: qsort (assert_smaller (x :: xs) (filter (>= x) xs)))
The expression assert_smaller (x :: xs) (filter (<= x) xs) asserts
that the result of the filter will always be smaller than the pattern
(x :: xs).
In more extreme cases, the function assert_total marks a
subexpression as always being total:
assert_total : a -> a
assert_total x = x
In general, this function should be avoided, but it can be very useful when reasoning about primitives or externally defined functions (for example from a C library) where totality can be shown by an external argument.
| [1] | Timothy G. Griffin. 1989. A formulae-as-type notion of control. In Proceedings of the 17th ACM SIGPLAN-SIGACT symposium on Principles of programming languages (POPL ‘90). ACM, New York, NY, USA, 47-58. DOI=10.1145/96709.96714 http://doi.acm.org/10.1145/96709.96714 |