Interactive Theorem Proving¶
Idris supports interactive theorem proving via elaborator reflection.
Elaborator Reflection Introduction is also used to convert high-level Idris code into the core language and for customising the language. Here we show how to use it to interactively construct proofs.
The primary purpose of the elaboration mechanism is to elaborate Idris and so it is not optimised to work as a proof assistant, however it can interactively construct proofs as described on this page.
Elab and Pruviloj Libraries¶
Elaborator reflection is defined in prelude/Language/Reflection/Elab.idr
and pruviloj is defined in Idris-dev/libs/pruviloj/.
Elab defines the basics such as: solve, attack, intro, compute,
rewriteWith and others.
pruviloj defines some more advanced derived commands such as:
reflexivity and others.
To use pruviloj call Idris with the -p pruviloj option and add:
import Pruviloj
import Pruviloj.Induction
to the top of your file.
It is useful to get the docs at the REPL by using the :doc command, and
search the docstrings using :apropos. So to introduce the functions from
Elab and Pruviloj, that we will need for the following example, here are
their docstrings:
*plusReducesZ> :doc solve
Language.Reflection.Elab.Tactics.solve : Elab ()
Substitute a guess into a hole.
*plusReducesZ> :doc attack
Language.Reflection.Elab.Tactics.attack : Elab ()
Convert a hole to make it suitable for bindings - that is, transform
it such that it has the form ?h : t . h as opposed to ?h : t . f h.
The binding tactics require that a hole be directly under its binding,
or else the scopes of the generated terms won't make sense. This
tactic creates a new hole of the proper form, and points the old hole
at it.
*plusReducesZ> :doc intro
Language.Reflection.Elab.Tactics.intro : (n : TTName) -> Elab ()
Introduce a lambda binding around the current hole and focus on the
body. Requires that the hole be in binding form (use attack).
Arguments:
n : TTName -- the name to use for the argument
*plusReducesZ> :doc compute
Language.Reflection.Elab.Tactics.compute : Elab ()
Normalise the goal.
*plusReducesZ> :doc rewriteWith
Language.Reflection.Elab.Tactics.rewriteWith : Raw -> Elab ()
Attempt to rewrite the goal using an equality.
The tactic searches the goal for applicable subterms, and constructs a
context for replace using them. In some cases, this is not possible,
and replace must be called manually with an appropriate context.
Because this tactic internally introduces a let binding, it requires
that the hole be immediately under its binder (use attack if it might
not be).
Here is the command from pruviloj that we will need for the example on
this page:
*plusReducesZ> :doc reflexivity
Pruviloj.Core.reflexivity : Elab ()
A special-purpose tactic that attempts to solve a goal using Refl.
This is useful for ensuring that goals in fact are trivial when
developing or testing other tactics; otherwise, consider using search.
Interactive Example: plusReduces¶
One way to write proofs interactively is to write the general structure of the proof, and use the interactive mode to complete the details. Consider the following definition, proved in Theorem Proving:
plusReduces : (n:Nat) -> plus Z n = n
We’ll be constructing the proof by induction, so we write the cases for Z
and S, with a recursive call in the S case giving the inductive
hypothesis, and insert holes for the rest of the definition:
import Pruviloj
import Pruviloj.Induction
plusReducesZ' : (n:Nat) -> n = plus n Z
plusReducesZ' Z = ?plusredZ_Z
plusReducesZ' (S k) = let ih = plusReducesZ' k in
?plusredZ_S
On running , two global names are created, plusredZ_Z and
plusredZ_S, with no definition.
*theorems> : idris plusReducesZ.idr -p pruviloj
. / _/___/ /____(_)____
/ // __ / ___/ / ___/ Version 1.2.0
_/ // /_/ / / / (__ ) https://www.idris-lang.org/
/___/\__,_/_/ /_/____/ Type :? for help
Idris is free software with ABSOLUTELY NO WARRANTY.
For details type :warranty.
Holes: Main.plusredZ_S, Main.plusredZ_Z
This tells us that we have two holes Main.plusredZ_S and Main.plusredZ_Z. We can solve
these separately, plusredZ_Z is the simplest so we will do that first.
The :elab plusredZ_Z command enters interactive elaboration mode, which can be used to
complete the missing definition for plusredZ_Z.
*plusReducesZ> :elab plusredZ_Z
---------- Goal: ----------
{hole_0} : 0 = 0
This has been normalised to 0 = 0 so now we have to prove that 0 equals 0, which
is easy to prove by reflexivity from the pruviloj library:
-Main.plusredZ_Z> reflexivity
plusredZ_Z: No more goals.
This tells us that the proof is complete. We can now leave the interactive mode which
we entered with the :elab command. We do this with the :qed command:
-Main.plusredZ_Z> :qed
Proof completed!
Main.plusredZ_Z = %runElab (do reflexivity)
Holes: Main.plusredZ_S
This gives us a trace of the proof which is plusredZ_Z = %runElab (do reflexivity). We
can cut & paste this into the hole in the original file. This also tells us that we
have another hole Main.plusredZ_S remaining.
This remaining proof is bit more complicated, the following diagram gives an overview:
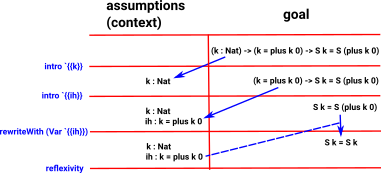
We approach this remaining proof in the same way by using the :elab command:
*plusReducesZ> :elab plusredZ_S
---------- Goal: ----------
{hole_0} : (k : Nat) -> (k = plus k 0) -> S k = S (plus k 0)
In this case, the goal is a function type, using k (the argument
accessible by pattern matching) and ih — the local variable
containing the result of the recursive call. We can introduce these as
assumptions using the intro tactic twice. The parameter is entered as
a constant of type TTName which is entered as a backtick with double
braces `{{ih}}. This gives:
-Main.plusredZ_S> intro `{{k}}
---------- Assumptions: ----------
k : Nat
---------- Goal: ----------
{hole_0} : (k = plus k 0) -> S k = S (plus k 0)
-Main.plusredZ_S> intro `{{ih}}
---------- Assumptions: ----------
k : Nat
ih : k = plus k 0
---------- Goal: ----------
{hole_0} : S k = S (plus k 0)
We know, from the type of ih, that k = plus k 0, so we would
like to use this knowledge to replace plus k 0 in the goal with
k. We can achieve this with the rewriteWith tactic:
-Main.plusredZ_S> rewriteWith (Var `{{ih}})
---------- Assumptions: ----------
k : Nat
ih : k = plus k 0
---------- Goal: ----------
{hole_0} : S k = S k
The rewriteWith tactic takes an equality proof as an argument, and tries
to rewrite the goal using that proof. The ih value is entered as a constant
of type TTName which is entered as a backtick with double braces `{{ih}} but
rewriteWith requires an expression of type Raw, rather than just a name,
so the Var constructor is used to make a variable. Here, it results in an equality
which is trivially provable using reflexivity:
-Main.plusredZ_S> reflexivity
plusredZ_S: No more goals.
-Main.plusredZ_S> :qed
Proof completed!
Main.plusredZ_S = %runElab (do intro `{{k}}
intro `{{ih}}
rewriteWith (Var `{{ih}})
reflexivity)
We can’t just cut & paste this into the hole in the original file like this:
import Pruviloj
import Pruviloj.Induction
%language ElabReflection
plusReducesZ' : (n:Nat) -> n = plus n Z
plusReducesZ' Z = %runElab (do reflexivity)
plusReducesZ' (S k) = let ih = plusReducesZ' k in
(%runElab (do intro `{{k}}
intro `{{ih}}
rewriteWith (Var `{{ih}})
reflexivity)
)
because this gives the following error:
Idris> :load elabInteractiveEx2.idr
elabInteractiveEx2.idr:10:32:
|
10 | intro `{{ih}}
| ^
unexpected "in"
expecting dependent type signature
However if we put the proof into a separate function like this:
import Pruviloj
import Pruviloj.Induction
%language ElabReflection
plusredZ_S : (k : Nat) -> (ih:(k = plus k Z)) -> (S k = S (plus k Z))
plusredZ_S = %runElab (do intro `{{k}}
intro `{{ih}}
rewriteWith (Var `{{ih}})
reflexivity)
plusReducesZ' : (n:Nat) -> n = plus n Z
plusReducesZ' Z = %runElab (do reflexivity)
plusReducesZ' (S k) = let ih = plusReducesZ' k in plusredZ_S k ih
This then loads [1] .
| [1] | https://github.com/idris-lang/Idris-dev/issues/4556 |