State¶
Many programs, even pure programs, can benefit from locally mutable state. For example, consider a program which tags binary tree nodes with a counter, by an inorder traversal (i.e. counting depth first, left to right). This would perform something like the following:
We can describe binary trees with the following data type BTree
and testTree to represent the example input above:
data BTree a = Leaf
| Node (BTree a) a (BTree a)
testTree : BTree String
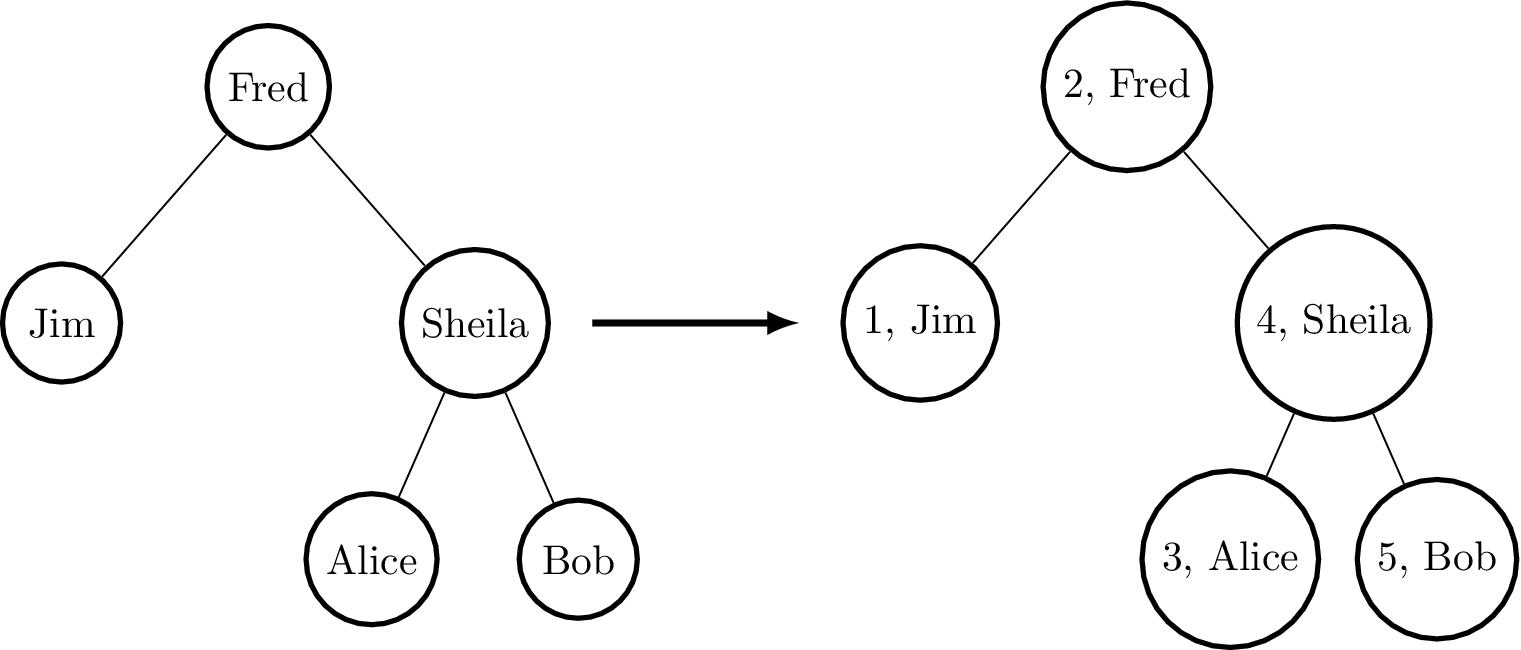
testTree = Node (Node Leaf "Jim" Leaf)
"Fred"
(Node (Node Leaf "Alice" Leaf)
"Sheila"
(Node Leaf "Bob" Leaf))
Then our function to implement tagging, beginning to tag with a
specific value i, has the following type:
treeTag : (i : Int) -> BTree a -> BTree (Int, a)
First attempt¶
Naïvely, we can implement treeTag by implementing a helper
function which propagates a counter, returning the result of the count
for each subtree:
treeTagAux : (i : Int) -> BTree a -> (Int, BTree (Int, a))
treeTagAux i Leaf = (i, Leaf)
treeTagAux i (Node l x r)
= let (i', l') = treeTagAux i l in
let x' = (i', x) in
let (i'', r') = treeTagAux (i' + 1) r in
(i'', Node l' x' r')
treeTag : (i : Int) -> BTree a -> BTree (Int, a)
treeTag i x = snd (treeTagAux i x)
This gives the expected result when run at the REPL prompt:
*TreeTag> treeTag 1 testTree
Node (Node Leaf (1, "Jim") Leaf)
(2, "Fred")
(Node (Node Leaf (3, "Alice") Leaf)
(4, "Sheila")
(Node Leaf (5, "Bob") Leaf)) : BTree (Int, String)
This works as required, but there are several problems when we try to
scale this to larger programs. It is error prone, because we need to
ensure that state is propagated correctly to the recursive calls (i.e.
passing the appropriate i or i’). It is hard to read, because
the functional details are obscured by the state propagation. Perhaps
most importantly, there is a common programming pattern here which
should be abstracted but instead has been implemented by hand. There
is local mutable state (the counter) which we have had to make
explicit.
Introducing Effects¶
Idris provides a library, Effects [3], which captures this
pattern and many others involving effectful computation [1]. An
effectful program f has a type of the following form:
f : (x1 : a1) -> (x2 : a2) -> ... -> Eff t effs
That is, the return type gives the effects that f supports
(effs, of type List EFFECT) and the type the computation
returns t. So, our treeTagAux helper could be written with the
following type:
treeTagAux : BTree a -> Eff (BTree (Int, a)) [STATE Int]
That is, treeTagAux has access to an integer state, because the
list of available effects includes STATE Int. STATE is
declared as follows in the module Effect.State (that is, we must
import Effect.State to be able to use it):
STATE : Type -> EFFECT
It is an effect parameterised by a type (by convention, we write
effects in all capitals). The treeTagAux function is an effectful
program which builds a new tree tagged with Ints, and is
implemented as follows:
treeTagAux Leaf = pure Leaf
treeTagAux (Node l x r)
= do l' <- treeTagAux l
i <- get
put (i + 1)
r' <- treeTagAux r
pure (Node l' (i, x) r')
There are several remarks to be made about this implementation.
Essentially, it hides the state, which can be accessed using get
and updated using put, but it introduces several new features.
Specifically, it uses do-notation, binding variables with <-,
and a pure function. There is much to be said about these
features, but for our purposes, it suffices to know the following:
doblocks allow effectful operations to be sequenced.x <- ebinds the result of an effectful operationeto a- variable
x. For example, in the above code,treeTagAux lis an effectful operation returningBTree (Int, a), sol’has typeBTree (Int, a).
pure eturns a pure valueeinto the result of an effectful- operation.
The get and put functions read and write a state t,
assuming that the STATE t effect is available. They have the
following types, polymorphic in the state t they manage:
get : Eff t [STATE t]
put : t -> Eff () [STATE t]
A program in Eff can call any other function in Eff provided
that the calling function supports at least the effects required by
the called function. In this case, it is valid for treeTagAux to
call both get and put because all three functions support the
STATE Int effect.
Programs in Eff are run in some underlying computation context,
using the run or runPure function. Using runPure, which
runs an effectful program in the identity context, we can write the
treeTag function as follows, using put to initialise the
state:
treeTag : (i : Int) -> BTree a -> BTree (Int, a)
treeTag i x = runPure (do put i
treeTagAux x)
We could also run the program in an impure context such as IO,
without changing the definition of treeTagAux, by using run
instead of runPure:
treeTagAux : BTree a -> Eff (BTree (Int, a)) [STATE Int]
...
treeTag : (i : Int) -> BTree a -> IO (BTree (Int, a))
treeTag i x = run (do put i
treeTagAux x)
Note that the definition of treeTagAux is exactly as before. For
reference, this complete program (including a main to run it) is
shown in Listing [introprog].
module Main
import Effects
import Effect.State
data BTree a = Leaf
| Node (BTree a) a (BTree a)
Show a => Show (BTree a) where
show Leaf = "[]"
show (Node l x r) = "[" ++ show l ++ " "
++ show x ++ " "
++ show r ++ "]"
testTree : BTree String
testTree = Node (Node Leaf "Jim" Leaf)
"Fred"
(Node (Node Leaf "Alice" Leaf)
"Sheila"
(Node Leaf "Bob" Leaf))
treeTagAux : BTree a -> Eff (BTree (Int, a)) [STATE Int]
treeTagAux Leaf = pure Leaf
treeTagAux (Node l x r) = do l' <- treeTagAux l
i <- get
put (i + 1)
r' <- treeTagAux r
pure (Node l' (i, x) r')
treeTag : (i : Int) -> BTree a -> BTree (Int, a)
treeTag i x = runPure (do put i; treeTagAux x)
main : IO ()
main = print (treeTag 1 testTree)
Effects and Resources¶
Each effect is associated with a resource, which is initialised
before an effectful program can be run. For example, in the case of
STATE Int the corresponding resource is the integer state itself.
The types of runPure and run show this (slightly simplified
here for illustrative purposes):
runPure : {env : Env id xs} -> Eff a xs -> a
run : Applicative m => {env : Env m xs} -> Eff a xs -> m a
The env argument is implicit, and initialised automatically where
possible using default values given by implementations of the following
interface:
interface Default a where
default : a
Implementations of Default are defined for all primitive types, and many
library types such as List, Vect, Maybe, pairs, etc.
However, where no default value exists for a resource type (for
example, you may want a STATE type for which there is no
Default implementation) the resource environment can be given explicitly
using one of the following functions:
runPureInit : Env id xs -> Eff a xs -> a
runInit : Applicative m => Env m xs -> Eff a xs -> m a
To be well-typed, the environment must contain resources corresponding
exactly to the effects in xs. For example, we could also have
implemented treeTag by initialising the state as follows:
treeTag : (i : Int) -> BTree a -> BTree (Int, a)
treeTag i x = runPureInit [i] (treeTagAux x)
Labelled Effects¶
What if we have more than one state, especially more than one state of
the same type? How would get and put know which state they
should be referring to? For example, how could we extend the tree
tagging example such that it additionally counts the number of leaves
in the tree? One possibility would be to change the state so that it
captured both of these values, e.g.:
treeTagAux : BTree a -> Eff (BTree (Int, a)) [STATE (Int, Int)]
Doing this, however, ties the two states together throughout (as well as not indicating which integer is which). It would be nice to be able to call effectful programs which guaranteed only to access one of the states, for example. In a larger application, this becomes particularly important.
The library therefore allows effects in general to be labelled so that they can be referred to explicitly by a particular name. This allows multiple effects of the same type to be included. We can count leaves and update the tag separately, by labelling them as follows:
treeTagAux : BTree a -> Eff (BTree (Int, a))
['Tag ::: STATE Int,
'Leaves ::: STATE Int]
The ::: operator allows an arbitrary label to be given to an
effect. This label can be any type—it is simply used to identify an
effect uniquely. Here, we have used a symbol type. In general
’name introduces a new symbol, the only purpose of which is to
disambiguate values [2].
When an effect is labelled, its operations are also labelled using the
:- operator. In this way, we can say explicitly which state we
mean when using get and put. The tree tagging program which
also counts leaves can be written as follows:
treeTagAux Leaf = do
'Leaves :- update (+1)
pure Leaf
treeTagAux (Node l x r) = do
l' <- treeTagAux l
i <- 'Tag :- get
'Tag :- put (i + 1)
r' <- treeTagAux r
pure (Node l' (i, x) r')
The update function here is a combination of get and put,
applying a function to the current state.
update : (x -> x) -> Eff () [STATE x]
Finally, our top level treeTag function now returns a pair of the
number of leaves, and the new tree. Resources for labelled effects are
initialised using the := operator (reminiscent of assignment in an
imperative language):
treeTag : (i : Int) -> BTree a -> (Int, BTree (Int, a))
treeTag i x = runPureInit ['Tag := i, 'Leaves := 0]
(do x' <- treeTagAux x
leaves <- 'Leaves :- get
pure (leaves, x'))
To summarise, we have:
:::to convert an effect to a labelled effect.:-to convert an effectful operation to a labelled effectful operation.:=to initialise a resource for a labelled effect.
Or, more formally with their types (slightly simplified to account only for the situation where available effects are not updated):
(:::) : lbl -> EFFECT -> EFFECT
(:-) : (l : lbl) -> Eff a [x] -> Eff a [l ::: x]
(:=) : (l : lbl) -> res -> LRes l res
Here, LRes is simply the resource type associated with a labelled
effect. Note that labels are polymorphic in the label type lbl.
Hence, a label can be anything—a string, an integer, a type, etc.
!-notation¶
In many cases, using do-notation can make programs unnecessarily
verbose, particularly in cases where the value bound is used once,
immediately. The following program returns the length of the
String stored in the state, for example:
stateLength : Eff Nat [STATE String]
stateLength = do x <- get
pure (length x)
This seems unnecessarily verbose, and it would be nice to program in a
more direct style in these cases. provides !-notation to help with
this. The above program can be written instead as:
stateLength : Eff Nat [STATE String]
stateLength = pure (length !get)
The notation !expr means that the expression expr should be
evaluated and then implicitly bound. Conceptually, we can think of
! as being a prefix function with the following type:
(!) : Eff a xs -> a
Note, however, that it is not really a function, merely syntax! In
practice, a subexpression !expr will lift expr as high as
possible within its current scope, bind it to a fresh name x, and
replace !expr with x. Expressions are lifted depth first, left
to right. In practice, !-notation allows us to program in a more
direct style, while still giving a notational clue as to which
expressions are effectful.
For example, the expression:
let y = 42 in f !(g !(print y) !x)
is lifted to:
let y = 42 in do y' <- print y
x' <- x
g' <- g y' x'
f g'
The Type Eff¶
Underneath, Eff is an overloaded function which translates to an
underlying type EffM:
EffM : (m : Type -> Type) -> (t : Type)
-> (List EFFECT)
-> (t -> List EFFECT) -> Type
This is more general than the types we have been writing so far. It is
parameterised over an underlying computation context m, a
result type t as we have already seen, as well as a List EFFECT and a
function type t -> List EFFECT.
These additional parameters are the list of input effects, and a list of output effects, computed from the result of an effectful operation. That is: running an effectful program can change the set of effects available! This is a particularly powerful idea, and we will see its consequences in more detail later. Some examples of operations which can change the set of available effects are:
- Updating a state containing a dependent type (for example adding an element to a vector).
- Opening a file for reading is an effect, but whether the file really is open afterwards depends on whether the file was successfully opened.
- Closing a file means that reading from the file should no longer be possible.
While powerful, this can make uses of the EffM type hard to read.
Therefore the library provides an overloaded function Eff
There are the following three versions:
SimpleEff.Eff : (t : Type) -> (input_effs : List EFFECT) -> Type
TransEff.Eff : (t : Type) -> (input_effs : List EFFECT) ->
(output_effs : List EFFECT) -> Type
DepEff.Eff : (t : Type) -> (input_effs : List EFFECT) ->
(output_effs_fn : x -> List EFFECT) -> Type
So far, we have used only the first version, SimpleEff.Eff, which
is defined as follows:
Eff : (x : Type) -> (es : List EFFECT) -> Type
Eff x es = {m : Type -> Type} -> EffM m x es (\v => es)
i.e. the set of effects remains the same on output. This suffices for
the STATE example we have seen so far, and for many useful
side-effecting programs. We could also have written treeTagAux
with the expanded type:
treeTagAux : BTree a ->
EffM m (BTree (Int, a)) [STATE Int] (\x => [STATE Int])
Later, we will see programs which update effects:
Eff a xs xs'
which is expanded to
EffM m a xs (\_ => xs')
i.e. the set of effects is updated to xs’ (think of a transition
in a state machine). There is, for example, a version of put which
updates the type of the state:
putM : y -> Eff () [STATE x] [STATE y]
Also, we have:
Eff t xs (\res => xs')
which is expanded to
EffM m t xs (\res => xs')
i.e. the set of effects is updated according to the result of the
operation res, of type t.
Parameterising EffM over an underlying computation context allows us
to write effectful programs which are specific to one context, and in some
cases to write programs which extend the list of effects available using
the new function, though this is beyond the scope of this tutorial.
| [1] | The earlier paper [3] describes the essential implementation details, although the library presented there is an earlier version which is less powerful than that presented in this tutorial. |
| [2] | In practice, ’name simply introduces a new empty type |
| [3] | (1, 2) Edwin Brady. 2013. Programming and reasoning with algebraic effects and dependent types. SIGPLAN Not. 48, 9 (September 2013), 133-144. DOI=10.1145/2544174.2500581 http://dl.acm.org/citation.cfm?doid=2544174.2500581 |