Generating Datatypes and Functions at Compile Time¶
Program elements, such as datatypes and functions can be constructed at compile-time in the Elab monad. This can allow proofs to be generated for user defined types or it could allow types to be automatically generated to support user defined types. An example is the code, from Elaborator reflection: extending Idris in Idris [1], that automatically generates accessibility predicates using the Bove-Capretta method.
Generating Datatypes¶
There are two main ‘tactics’ associated with generating datatypes:
- declareDatatype
- defineDatatype
Which declare and define the datatype as the names suggest.
| These ‘tactics’ and the data structures associated with them are listed in the tables later on this page, for now, here is a summary: | 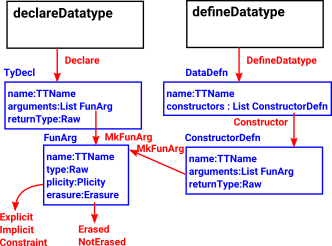
|
| As a first example, the following boolean-like type can be constructed. When the compiler has run it will be available to us as if we had compiled it in the usual way: | λΠ> :printdef Two
data Two : Type where
F : Two
T : Two
|
This was generated by the following code:
module TwoDef
%language ElabReflection
addTwo : Elab ()
addTwo = do let twoname : TTName = `{{TwoDef.Two}}
let F2 = `{{TwoDef.F}}
let T2 = `{{TwoDef.T}}
declareDatatype $ Declare twoname [] `(Type)
defineDatatype $ DefineDatatype twoname [
Constructor `{{F}} [] (Var `{{TwoDef.Two}}),
Constructor `{{T}} [] (Var `{{TwoDef.Two}})
]
%runElab addTwo
| The constructors T and F can be called as would be expected: | λΠ> F
F : Two
λΠ> T
T : Two
|
Generating Functions¶
There are two main ‘tactics’ associated with generating functions:
- declareType
- defineFunction
Which declare and define the function as the names suggest.
| These ‘tactics’ and the data structures associated with them are listed in the tables later on this page, for now, here is a summary: | 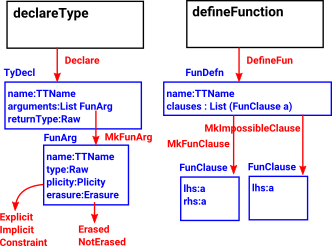
|
Note: The left hand side (lhs) and right hand side (rhs) of FunClause typically is of type ‘Raw’.
| Bound pattern variables are represented by ‘PVar’ binders: This diagram shows an example of a possible Raw structure that might be used in a function definition. | 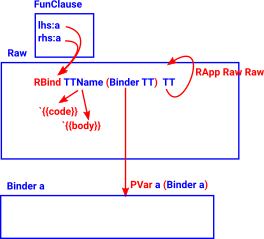
|
| Some function definitions can now be added to the above datatype. This is what they will look like: | λΠ> :printdef perm1
perm1 : Two -> Two
perm1 F = F
perm1 T = T
λΠ> :printdef perm2
perm2 : Two -> Two
perm1 F = T
perm1 T = F
|
This was generated with the following code:
let perm1 = `{{TwoDef.perm1}}
declareType (Declare perm1 [MkFunArg `{{code}} (Var twoname) Explicit NotErased] (Var twoname))
defineFunction $ DefineFun perm1 [
MkFunClause (RApp (Var perm1) (Var `{{TwoDef.F}})) (Var F2),
MkFunClause (RApp (Var perm1) (Var `{{TwoDef.T}})) (Var T2)
]
let perm2 = `{{TwoDef.perm2}}
declareType (Declare perm2 [MkFunArg `{{code}} (Var twoname) Explicit NotErased] (Var twoname))
defineFunction $ DefineFun perm2 [
MkFunClause (RApp (Var perm1) (Var `{{TwoDef.F}})) (Var T2),
MkFunClause (RApp (Var perm1) (Var `{{TwoDef.T}})) (Var F2)
]
| This is what happens when we call the functions: | λΠ> perm1 F
F : Two
λΠ> perm1 T
T : Two
λΠ> perm2 F
T : Two
λΠ> perm2 T
F : Two
|
So far these datatypes and functions could have been written, statically, in the usual way. However, it is possible to imagine situations where we may need a lot of functions to be generated automatically at compile time. For example, if we extend this Boolean datatype to a datatype with more simple constructors (a finite set), we could generate a function for every possible permutation of that datatype back to itself.
A Different Example which has Type Parameters¶
| Here is an example of a datatype with type parameters: | data N : Nat -> Type where
MkN : N x
MkN' : (x : Nat) -> N (S x)
|
This was produced by the following code:
module DataDef
%language ElabReflection
addData : Elab ()
addData = do
let dataname : TTName = `{{DataDef.N}}
declareDatatype $ Declare dataname [MkFunArg `{{n}} `(Nat) Explicit NotErased] `(Type)
defineDatatype $ DefineDatatype dataname [
Constructor `{{MkN}} [MkFunArg `{{x}} `(Nat) Implicit NotErased]
(RApp (Var dataname) (Var `{{x}})),
Constructor `{{MkN'}} [MkFunArg `{{x}} `(Nat) Explicit NotErased]
(RApp (Var dataname) (RApp (Var `{S}) (Var `{{x}})))
]
%runElab addData
So this declares and defines the following data structure ‘N’ with a constructor ‘MkN’ which can have an implicit or an explicit Nat argument. Which can be used like this:
λΠ> :t N
N : Nat -> Type
λΠ> N 2
N 2 : Type
λΠ> N 0
N 0 : Type
λΠ> :t MkN
MkN : N x
Table of ‘tactics’ for Generating Data and Functions¶
These are the functions that we can use to create data and functions in the Elab monad:
| declareType | Add a type declaration to the global context. Signature: declareType : TyDecl -> Elab () |
|---|---|
| defineFunction | Define a function in the global context. The function must have already been declared, either in ordinary Idris code or using declareType. Signature: defineFunction : FunDefn Raw -> Elab () |
| declareDatatype | Declare a datatype in the global context. This step only establishes the type constructor; use defineDatatype to give it constructors. Signature: declareDatatype : TyDecl -> Elab () |
| defineDatatype | Signature: defineDatatype : DataDefn -> Elab () |
| addImplementation | Register a new implementation for interface resolution. Arguments:
Signature: addImplementation : (ifaceName, implName : TTName) -> Elab () |
| isTCName | Determine whether a name denotes an interface. Arguments:
Signature: isTCName : (name : TTName) -> Elab Bool |
Table of Datatypes Associated with Generating Data and Functions¶
The above functions use the following data/records:
| Plicity | How an argument is provided in high-level Idris data Plicity=
||| The argument is directly provided at the application site
Explicit |
||| The argument is found by Idris at the application site
Implicit |
||| The argument is solved using interface resolution
Constraint
|
|---|---|
| FunArg | Function arguments These are the simplest representation of argument lists, and are used for functions. Additionally, because a FunArg provides enough information to build an application, a generic type lookup of a top-level identifier will return its FunArgs, if applicable. record FunArg where
constructor MkFunArg
name : TTName
type : Raw
plicity : Plicity
erasure : Erasure
|
| TyConArg | Type constructor arguments Each argument is identified as being either a parameter that is consistent in all constructors, or an index that varies based on which constructor is selected. data TyConArg =
||| Parameters are uniform across the constructors
TyConParameter FunArg |
||| Indices are not uniform
TyConIndex FunArg
|
| TyDecl | A type declaration for a function or datatype record TyDecl where
constructor Declare
||| The fully-qualified name of the function or datatype being declared.
name : TTName
||| Each argument is in the scope of the names of previous arguments.
arguments : List FunArg
||| The return type is in the scope of all the argument names.
returnType : Raw
|
| FunClause | A single pattern-matching clause data FunClause : Type -> Type where
MkFunClause : (lhs, rhs : a) -> FunClause a
MkImpossibleClause : (lhs : a) -> FunClause a
|
| FunDefn | A reflected function definition. record FunDefn a where
constructor DefineFun
name : TTName
clauses : List (FunClause a)
|
| ConstructorDefn | A constructor to be associated with a new datatype. record ConstructorDefn where
constructor Constructor
||| The name of the constructor. The name must _not_ be qualified -
||| that is, it should begin with the `UN` or `MN` constructors.
name : TTName
||| The constructor arguments. Idris will infer which arguments are
||| datatype parameters.
arguments : List FunArg
||| The specific type constructed by the constructor.
returnType : Raw
|
| DataDefn | A definition of a datatype to be added during an elaboration script. record DataDefn where
constructor DefineDatatype
||| The name of the datatype being defined. It must be
||| fully-qualified, and it must have been previously declared as a
||| datatype.
name : TTName
||| A list of constructors for the datatype.
constructors : List ConstructorDefn
|
| CtorArg | CtorParameter data CtorArg = CtorParameter FunArg | CtorField FunArg
|
| Datatype | A reflected datatype definition record Datatype where
constructor MkDatatype
||| The name of the type constructor
name : TTName
||| The arguments to the type constructor
tyConArgs : List TyConArg
||| The result of the type constructor
tyConRes : Raw
||| The constructors for the family
constructors : List (TTName, List CtorArg, Raw)</td>
|
| [1] | https://dl.acm.org/citation.cfm?doid=2951913.2951932 |